

You can determine what happens to the wave function when you swap particles in a multi-particle atom. Whether the wave function is symmetric or antisymmetric under such operations gives you insight into whether two particles can occupy the same quantum state.
Given that Pij 2 = 1, note that if a wave function is an eigenfunction of Pij, then the possible eigenvalues are 1 and –1. That is, for
![]()
an eigenfunction of Pij looks like
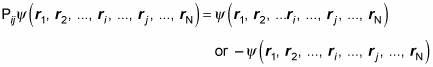
That means there are two kinds of eigenfunctions of the exchange operator:
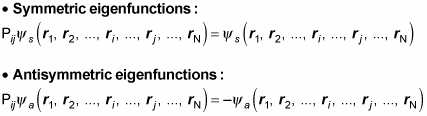
Now take a look at some symmetric and some antisymmetric eigenfunctions. How about this one — is it symmetric or antisymmetric?
You can apply the exchange operator P12:
![]()
Note that because
![]()
is a symmetric wave function; that’s because
![]()
How about this wave function?
Again, apply the exchange operator, P12:
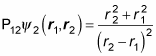
Okay, but because
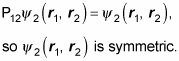
Here’s another one:
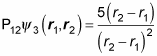
How does that equation compare to the original one? Well,
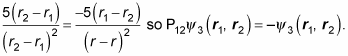
What about this one?
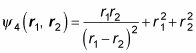
To find out, apply P12:
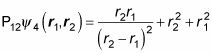
All right — how’s this compare with the original equation?
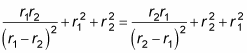
You may think you have this process down pretty well, but what about this next wave function?
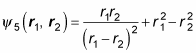
Start by applying P12:
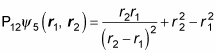
So how do these two equations compare?
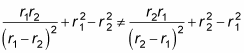
is neither symmetric nor antisymmetric. In other words,
is not an eigenfunction of the P12 exchange operator.
Steven Holzner is an award-winning author of technical and science books (like Physics For Dummies and Differential Equations For Dummies). He graduated from MIT and did his PhD in physics at Cornell University, where he was on the teaching faculty for 10 years. He’s also been on the faculty of MIT. Steve also teaches corporate groups around the country.